www.epsilon-lyrae.de
zum Artikel 61 Cygni zurück
Porträt Bessels
Kontakt
Datenschutzerklärung



Ernst Florens Friedrich Chladni
Die Akustik 1830


Titelseite



Seite 288



Seite 296



Seite 300



Seite 316
 Eigenschwingungsformen von runden Platten

Ein Anwendungsbeispiel für die Besselfunktionen : Chladnische Klangfiguren

Die Eigenschwingungsformen von Platten hängen von deren Geometrie und den Randbedingungen ab. Der Modus der Eigenschwingung wird bei runden Platten durch die Anzahl der Knotendurchmesser und die Anzahl der Knotenkreise charakterisiert. Die Anzahl der Knotendurchmesser wird durch die Ordnung der Bessel- bzw. der modifizierten Besselfunktionen beschrieben. Die Anzahl der Knotenkreise korrespondiert mit der Zahl der Nullstellen dieser Funktionen.

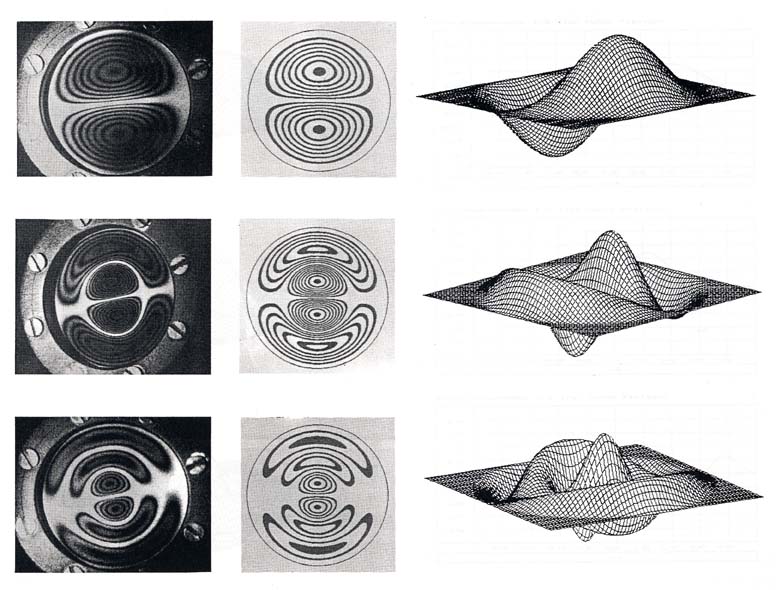
Besselfunktion, Holografie, Time Average Verfahren, Plattenschwingungen, Knotenkreise, Knotendurchmesser
a) Holografische Interferogramme im Time Average Verfahren, b) berechnete Interferogramme, c) 3D-Simulationen der Eigenschwingungsformen, J.S. Schlimmer 1993

Die erste Spalte der Abbildung zeigt Holografische Interferogramme einer allseitig, fest eingespannten, runden Platte. Die Interferogramme wurden im Time Average Verfahren hergestellt. Der Kontrast dieses Verfahrens entspricht bei Eigenschwingungen dem Quadrat der Besselfunktion 0-ter Ordnung. Schwingungsknoten werden hell dargestellt (relative Maxima der Besselfunktion), während die Schwingungsbäuche schwarz erscheinen (Nullstellen der Besselfunktion). Bei den hier gezeigten Eigenschwingungen handelt es sich um Schwingungen im (1,0)-Modus, (1,1)-Modus und (1,2)-Modus.

Die zweite Spalte zeigt die Berechnung der entsprechenden Interferenzlinienverläufe (Nullstellen). Zur Berechnung des Interferenzlinienverlaufs müssen anschließend die Funktionswerte der Eigenschwingung mit dem Kontrast des Time-Average Verfahrens korreliert werden.

Die dritte Spalte zeigt eine 3D-Darstellung der Eigenschwingungsformen. Die Amplitude ist stark überhöht dargestellt. In Wirklichkeit geht man davon aus, dass die Schwingungsamplitude klein gegenüber der Plattendicke ist.


Besselfunktion

Besselfunktionen erster Gattung n-ter Ordnung :



Modifizierte Besselfunktionen n-ter Ordnung :


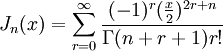
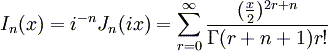
Die Besselfunktionen lassen sich näherungsweise als endliche Reihen berechnen oder durch numerische Integration lösen. Weitere Informationen : siehe Wikipedia : Besselsche Differentialgleichung

Seitenaufrufe seit 15. Juli 2005 :