Inhalt :

• Einleitung
• Das Auflösungsvermögen eines 8 Zoll Teleskops
• Entstehung und Eigenschaften des Seeing
• Der Einfluß des Beobachtungsortes auf das Seeing
• Die Modulations Transfer Funktion (MTF)
• Die Messung der MTF
• Ergebnisse
• Fehlerbetrachtung
• Zusammenfassung
• Danksagung
• Anhang
• Literatur
  

Stichworte : Seeing, Strahlungsnächte, Kohärenzlänge, Modulations Transfer Funktion (MTF), Interferometrie

von J. S. Schlimmer (aus NightSky 2/2004)

Einleitung

Neben der Optik und der Art des Detektors (Auge, Film, CCD) hat die Luftunruhe einen entscheidenden Einfluss auf die Qualität der Abbildung. Neben der Bildschärfe ist vor allem der Kontrast betroffen. Während Optiken und Detektoren oft beschrieben und diskutiert werden, wird die Luftunruhe in der Regel als gegeben hingenommen und vernachlässigt. Wie sich die Luftunruhe auf eine Abbildung auswirkt, soll im folgenden Artikel näher dargestellt werden.

Das Auflösungsvermögen eines 8-Zoll-Teleskops

Legt man eine Wellenlänge von 500 nm zugrunde, so ergibt sich für ein Teleskop mit 8-Zoll Öffnung nach dem Rayleigh - Kriterium eine theoretische Auflösung von 0,63 Bogensekunden. Bei dem Rayleigh - Kriterium geht man davon aus, dass sich zwei Beugungsscheibchen gleicher Helligkeit und Farbe noch trennen lassen, wenn das Minimum des ersten mit dem Maximum des zweiten zusammenfällt. Zwischen den beiden sich überlappenden Beugungsscheibchen fällt die Helligkeit auf 75 % des Maximalwertes ab. Dies entspricht immerhin noch einem Kontrast von rund 14 %. 
Das Auflösungskriterium von Rayleigh stammt zwar aus dem Bereich der Spektroskopie, lässt sich aber zum Beispiel sehr gut auf die Trennung von Doppelsternen anwenden. Man sollte dieses Kriterium aber generell nur als Anhaltspunkt betrachten. Bei diesen Überlegungen ist die Luftunruhe, die nachfolgend als Seeing bezeichnet wird, noch nicht berücksichtigt.

Entstehung und Eigenschaften des Seeings

Unter dem Begriff Seeing versteht man allgemein das Flimmern und Funkeln der Sterne, welche durch Effekte der turbulenten Erdatmosphäre hervorgerufen werden. In der Literatur wird oft zwischen einem Seeing- und einem Szintillationsanteil unterschieden. Der Seeinganteil bezieht sich dabei auf die Ortsschwankungen während der Szintillationsanteil die Helligkeitsschwankungen beschreibt. Beide Effekte werden durch Luftturbulenzen verursacht. Die Luftturbulenzen entstehen an der Grenze zwischen den Luftschichten der Atmosphäre und werden durch unterschiedliche Temperaturen hervorgerufen. Warme Luft hat eine geringere Dichte als kalte Luft. Dadurch steigen warme Luftmassen auf und es kommt zu einer ständigen Mischung. Diese Luftmassen kann man sich statistisch wie Zellen oder Blasen vorstellen [1]. Mit der Dichte der einzelnen Luftzellen verändert sich auch der Brechungsindex und somit ändert sich auch ständig die Richtung eines Lichtstrahls (Ortsschwankungen). Ferner kann die Phasendifferenz zwischen zwei benachbarten Lichtwellen gerade so groß sein, dass es zur Auslöschung kommt (Helligkeitsschwankungen). In Abbildung 1 sind diese beiden Effekte gut zu sehen. Mit zunehmender Öffnung des Teleskops nimmt der Effekt des Seeings zu, da die Phasenbeziehungen der zur Abbildung beitragenden Lichtwellen immer stärker gestört werden.

Die Phasendifferenz zweier Lichtwellen wird allgemein auch als Gangunterschied bezeichnet. Wird der Gangunterschied zwischen einzelnen Lichtwellen zu groß, so besteht zwischen ihnen keine räumliche Beziehung mehr. Der Physiker D. L. Fried führte 1965 hierzu die Kohärenzlänge r0 ein, die angibt wie groß der maximale Abstand zweier Lichtwellen noch sein darf, damit die Störungen der Luftbewegungen noch vernachlässigt werden können. Die Kohärenzlänge r0, die auch als Fried Parameter bezeichnet wird, beschreibt letztlich die effektive Öffnung, bei der ein Teleskop noch beugungsbegrenzt abbildet !
Vereinfacht kann man sich die Kohärenzlänge als die durchschnittliche Größe der einzelnen Luftzellen vorstellen. Typische Werte sind 5 bis 15 cm. Ist die Öffnung eines Teleskops sehr viel größer wie die Kohärenzlänge, zerfällt das Seeingscheibchen in einzelne Speckles (Flecken) [1]. Generell wächst das Seeing in Abhängigkeit von der Zenitdistanz (Abbildung 2, siehe hinten Formel A1) [2,3].

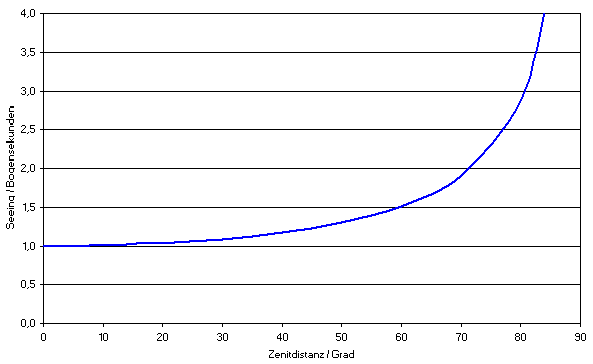
Abbildung 2 : Das Seeing in Abhängigkeit von der Zenitdistanz (Abstand vom Zenit), bei einem angenommenen Seeing von 1 Bogensekunde im Zenit. In Horizontnähe ist das Seeing am schlechtesten.

Durch das Seeing wird bei der Astrofotografie eine Punktquelle (Stern) in ein Seeingscheibchen umgewandelt. Dadurch wird das Auflösungsvermögen eines Teleskops zusätzlich begrenzt. Durch Techniken wie z. B. der adaptiven Optik ist es seit einigen Jahren möglich, das Auflösungsvermögen der Großteleskope deutlich über die Begrenzungen des Seeings zu verbessern. Auch in der Amateurastronomie ist es durch den Einsatz preiswerter Webcams in Verbindung mit speziellen Softwarealgorithmen möglich geworden, die Effekte des Seeings teilweise zu kompensieren. Die Erfolge sind zum Teil so enorm, dass sie den direkten Vergleich mit Aufnahmen des Hubble Teleskops erlauben [4].

Der Einfluss des Beobachtungsortes auf das Seeing

Neben den atmosphärischen Bedingungen in den hohen Luftschichten hat auch der Beobachtungsort einen großen Einfluss auf das Seeing. Betrachten wir zunächst eine größere Stadt in einer Ebene. Städte weisen an sonnigen Tagen eine deutlich höhere Oberflächentemperatur als das sie umgebende Freiland auf. Man bezeichnet sie daher auch als Wärmeinseln. Dies führt zu einer starken Erwärmung der Luft, die über den Städten mehrere hundert Meter aufsteigt [5]. Dieser Vorgang läuft bis tief in die Nacht ab. Erst in der zweiten Nachthälfte stellt sich in wolkenlosen, windstillen Nächten - den so genannten Strahlungsnächten - eine labile Schichtung ein. Im Freiland hingegen schichtet sich die Luft bereits nach Sonnenuntergang entsprechend ihrer spezifischen Dichte. Die Luft ist hier weitaus weniger turbulent, wie in der Stadt.
Verlegen wir nun unseren Beobachtungsort von der Stadt ins Mittelgebirge. Auf den Kuppen der Hügel ist es tagsüber deutlich kälter wie in den Tälern, oder gar in der Ebene. In Strahlungsnächten kühlt sich die Temperatur auf den Bergkuppen allerdings nur gering ab. Kurz nach Sonnenuntergang hat die Temperatur schon nahezu ihr Minimum erreicht ! In den Tälern hingegen kühlt sich die Temperatur während der ganzen Nacht kontinuierlich ab und erreicht erst kurz vor Sonnenaufgang ihr Minimum. Der Grund hierfür liegt wiederum in der spezifischen Dichte der Luft. Auf den Kuppen fließt die Kaltluft abwärts ins Tal und wird durch Luft der freien Atmosphäre der Umgebung ersetzt. Dieser Luftaustausch führt dazu, dass die Temperatur der bodennahen Luft auf den Bergkuppen die ganze Nacht über nahezu konstant ist. In den Tälern wo die Kaltluft nicht mehr weiter abfließen kann, entsteht ein so genannter Kaltluftsee. Sinkt die Temperatur unter den Taupunkt kommt es hier zur Nebelbildung. Auf Bergkuppen hat man daher auch viel weniger Probleme mit Taubeschlag der Optiken ! Im Sommer betragen die Temperaturdifferenzen zwischen Tages- und Nachtwert in der oberrheinischen Tiefebene bis zu 15 K. Auf dem Feldberg im Schwarzwald (1500 m N.N.) hingegen beträgt die Differenz lediglich 5 K [6]. Diese Effekte lassen sich schon bei sehr viel niedrigeren Hügeln beobachten. Der geringe Temperaturunterschied zwischen Tages- und Nachtwert auf den Bergkuppen führt zu einer geringeren konvektiven Erwärmung der Luft, was sich nachts positiv auf das Seeing auswirkt. Auch die Temperaturkonstanz ist nicht nur für den Beobachter angenehm, sie ermöglicht eine bessere Anpassung der Spiegeltemperatur an die Umgebungstemperatur was sich positiv auf das Tubusseeing [7] auswirkt. Diese Strahlungseffekte lassen sich sehr leicht mit Hilfe eines Außenthermometers am Auto beobachten. Fährt man nach einer Beobachtungsnacht nach Hause, so nimmt die Temperatur ab, je geringer die Höhe wird.

Die Modulations Transfer Funktion (MTF)

Die Güte einer Abbildung hängt von dem Auflösungsvermögen (Schärfe) und dem Kontrast des Übertragungssystems ab. Bei der Modulations Transfer Funktion (MTF) werden beide Größen gleichzeitig berücksichtigt. Sie wird daher auch oft als Kontrast Übertragungs Funktion oder kurz als Kontrastfunktion bezeichnet. Beim Seeing handelt es sich um eine statistische Größe, die primär bei der Astrofotografie eine Rolle spielt und sich hierfür gut beschreiben lässt. Zur Beschreibung des Seeings kann die zeitlich gemittelte MTF mit Hilfe der Kohärenzlänge ausgedrückt werden (Formel A2) [2]. Seeing und Kohärenzlänge sind über die Wellenlänge miteinander verknüpft (Formel A3). Für eine Wellenlänge von 500 nm ergibt sich für das Seeing von 1 Bogensekunde eine Kohärenzlänge von rund 10 cm (siehe Beispiel Formel A3). Bei sehr günstigen Beobachtungsverhältnissen kann das Seeing im Zenit Werte um 1 Bogensekunde erreichen. Für horizontnahe Objekte ergeben sich dann schnell Werte von 2 und mehr Bogensekunden (siehe Abbildung 2). Bei durchschnittlichen Beobachtungsbedingungen kann man im Zenit von einem Seeing zwischen 1 und 2 Bogensekunden ausgehen. In Abbildung 3 ist die berechnete MTF für ein Seeing von 1 und 2 Bogensekunden dargestellt. 

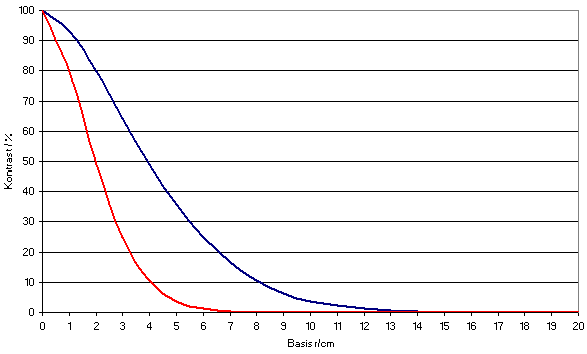
Abbildung 3 : Die MTF für ein Seeing von 1 Bogensekunde (blaue Linie) und 2 Bogensekunden (rote Linie). 

Aus Abbildung 3 geht deutlich hervor, dass das maximale Auflösungsvermögen bei der Fotografie in der Praxis schon mit einem 4-Zoll Teleskop (Basis 10 cm) nahezu erreicht wird. Der Kontrast der Abbildung ist dann bereits auf 3,8 % gefallen. Zum Glück gilt diese Aussage nur für zeitlich gemittelte Werte und nicht für die visuelle Beobachtung.
Bei der Astrofotografie kann man sich das atmosphärische Seeing wie ein Tiefpass Filter vorstellen : hohe Frequenzen werden zunehmend unterdrückt, während niedrige Frequenzen passieren können. Die Atmosphäre verhindert also hoch aufgelöste, langzeit belichtete Astroaufnahmen.
Bei der visuellen Beobachtung oder der Videoastronomie hat die hier dargestellte MTF keine Gültigkeit, da die momentanen Störungen darin nicht beschrieben werden.  Mit den kurzen Belichtungszeiten von Webcams ist es möglich, das Seeing einzufrieren und die besten Abbildungen im Nachhinein zu verarbeiten. Dies kann man sich zum Beispiel bei der Aufzeichnung von Mondlandschaften (siehe Abbildung 6) zu Nutze machen.

Die Messung der MTF

Doch nun zurück zur Praxis. Die Messung der MTF ist im Grunde recht einfach und geschieht mit Hilfe einer Doppellochblende, die auch als Scheinerblende bekannt ist. Durch die Blende wird das Teleskop zu einem einfachen Fizeau Interferometer. Die Lichtwellen beider Öffnungen überlagern im Fokus miteinander und es entsteht ein typisches Interferenzmuster, dessen Streifendichte vom Abstand der Öffnungen abhängt. Der Kontrast (Formel A4) der Streifen hängt von der räumlichen Kohärenz ab und diese wiederum ist ein Maß für die MTF. Eine ausführliche Beschreibung eines Fizeau Interferometers findet der interessierte Leser in [8]. 
Die Scheinerblende ist so angefertigt, dass der Abstand der Öffnungen beliebig variiert werden kann. Mit einem Durchmesser von 22 mm sind die Öffnungen einerseits so gewählt, dass das entstehende Beugungsscheibchen möglichst groß wird und andererseits noch genug Licht ins Teleskop gelangt. Natürlich kann man die Öffnungen auch kleiner gestalten. Die Größe und Art des Teleskops hat keinen Einfluss auf das Ergebnis !
Ein orange-rot Filter grenzt das Spektrum ein, wodurch die Interferenzstreifen deutlicher hervortreten. Im Fokus des Teleskops befindet sich eine Webcam, mit der die Interferogramme als Video aufgenommen werden. Als Stern kommen grundsätzlich alle hellen Sterne in Frage, die in Zenitnähe stehen.  In 10 Sekunden werden 100 Einzelbilder in den Computer eingelesen. Zur Auswertung werden später die Einzelbilder der jeweiligen Videos ohne weitere Objektzentrierung miteinander überlagert (Abbildung 4). Hierfür stehen verschiedene Programme im Internet kostenlos zur Verfügung [9,10]. 

Aus den Helligkeiten der Interferenzstreifen kann der Kontrast ermittelt werden. Der Kontrast kann dabei Werte zwischen 0 und 100 % annehmen. Zur Ermittlung des Kontrastes werden die Bilder nicht aufbereitet, die Hintergrundhelligkeit (Rauschen) muss berücksichtigt werden. 

Ergebnisse 

In Abbildung 5 sind die ermittelten Streifenkontraste als rote Punkte dargestellt. Diese können durch eine MTF mit einer Kohärenzlänge von 16 cm am Besten angenähert werden (schwarze Linie). Mit einer Belichtungszeit von 1/25 Sekunden für ein Einzelbild ergibt sich eine Gesamtbelichtungszeit von gerade mal 4 Sekunden. Eine Kohärenzlänge von 16 cm entspricht bei einer Wellenlänge von 620 nm (orangerot Filter) einem Seeing von 0,80 Bogensekunden. Der Stern Vega, der für die Messungen verwendet wurde, stand zu diesem Zeitpunkt 17° vom Zenit entfernt. Für den Zenit ergibt sich damit ein Seeing von  0,78 Bogensekunden ! Längere Belichtungszeiten hätten zu einem schlechteren Ergebnis geführt. Dennoch lassen sich die ermittelten Streifenkontraste bereits sehr gut für kurze Belichtungszeiten mit der theoretisch berechneten MTF angleichen. 

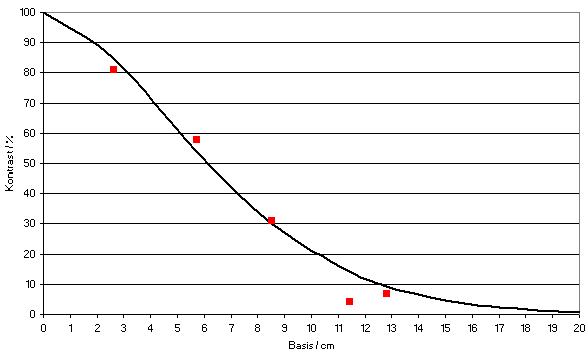
Abbildung 5 : Vergleich der gemessenen Kontraste (rote Punkte) mit der berechneten MTF Kurve für r0 = 16 cm (Linie), Belichtungszeit : 4 s

Abbildung 6 zeigt eine Aufnahme der Region um den Mond Krater Ptolemäus, der am Rande des Terminators liegt. Bei dem Krater Arzachel ist der Zentralberg bereits sehr schön zu sehen, da er von der Sonne beschienen wird, während das Innere des Kraters noch im Schatten liegt. Auch die höchsten Bergspitzen des Kap Taenarium werden bereits sichtbar. Für dieses Bild wurden die 14 besten Einzelbilder einer kurzen Videosequenz miteinander überlagert [9]. Der Bildausschnitt beträgt etwa 900 km x 675 km. Die Brennweite der Aufnahme betrug lediglich 1500 mm wodurch sich das Seeing nicht zu stark auf die Abbildung auswirkte.

Fehlerbetrachtung

Auf eine Abbildung wirkt sich natürlich nicht nur die MTF der Luft aus. Jede abbildende Komponente hat ihre eigene Kontrastfunktion und auch der Empfänger überträgt die Bildinformationen auf eine bestimmte, mit Verlusten und Fehlern behaftete Weise (siehe Artikel Vixen Newton R200SS (200/800) mit Koma Korrektor). Der Kontrast des CCD Chips verschlechtert sich mit zunehmender Streifendichte des Interferograms. Die Interferogramme in Abbildung 4 sind also das Ergebnis der Übertragungskette, die sich aus Atmosphäre, Optik (2 Barlowlinsen, 1 Filterglas) und CCD-Chip zusammensetzt. 

Zusammenfassung

Das Seeing wirkt sich auf den Kontrast der Abbildung in der visuellen und der fotografischen Astronomie völlig unterschiedlich aus und hängt maßgeblich von der Belichtungszeit ab. Für Belichtungszeiten von 4 Sekunden kann bereits die von Fried beschriebene Modulations Transfer Funktion verwendet werden um die gefundenen Kontraste zu beschreiben. Mit Hilfe von Webcams können kurzzeitbelichtete Aufnahmen angefertigt werden mit denen das Seeing quasi eingefroren werden kann. Für Einzelbilder kann somit ein Kontrast gefunden werden, der weitestgehend von der Optik und dem CCD Chip abhängt. 

Danksagung

Mein Dank gilt allen Softwareentwicklern, die so freundlich waren, Ihre Programme kostenlos im Internet zur Verfügung zu stellen. Ohne diese Programme wäre der sinnvolle Einsatz der Videoastronomie nicht möglich. 

• A1) Abhängigkeit des Seeings omega von der Zenitdistanz z [2,3] : omega(Zenit) = omega(z) 1/cos(z)^3/5 [z ist im Bogenmaß einzugeben]
• A2) Die zeitlich gemittelte MTF in Abhängigkeit der Kohärenzlänge r0 [2] : MTF(r0)= exp [-3,44 (Basis/r0)^5/3] 
• A3) Zusammenhang zwischen Kohärenzlänge und dem Seeingscheibchen [2] : r0 = omega/lambda, Beispiel : r0 = 500 *10^(-9) m / (1,0 *360°/2Pi *3600“) =0.103 m
• A4) Der Kontrast wie folgt berechnet : k = (Imax – Imin) / (Imax + Imin), mit Imax : maximale Helligkeit der Interferenzstreifen, Imin : minimale Helligkeit des benachbarten Streifens

[1] A. Glindermann und A. Quirrenbach, Künstlicher Stern über dem Calar Alto Sterne und Weltraum 11/1997
[2] Paul Titze, A Seeing Analyses for SUSI, http://www.physics.usyd.edu.au/~ptitze/work/seeing.htm
[3] The Intrinsic Seeing Quality at the WHT Site, http://www.ing.iac.es/Astronomy/development/hap/dimm.html
[4] R. Schulz, H. Csadek, Die Marsopposition 2001, Sterne und Weltraum 12/2001
[5] F. Fezer, Das Klima der Städe, Justus Perthes Verlag Gotha GmbH, 1995
[6] H.P.Tamm, Modellierung von Flächendatensätzen der Oberflächentemperatur, Strahlungsbilanz und Kaltluftproduktion in Strahlungsnächten, Dissertation, Uni Freiburg, 2000, http://www.freidok.uni-freiburg.de/volltexte/26/pdf/26_1.pdf
[7] J. S. Schlimmer, Ein Lüfter an einem 8-Zoll-Newton-Teleskop, Sterne und Weltraum 6/2002
[8] Franz Kerschbaum, Ein visuelles Stern-Interferometer im Eigenbau, Sterne und Weltraum 4/1999
[9] avi2bmp, http://avi2bmp.free.fr/
[10] Robert J. Stekelenburg, AstroStack 2, http://www.astrostack.com/

zum Seitenanfang zurück

Seitenaufrufe seit 1. Januar 2005 :