www.epsilon-lyrae.de
zur Startseite zurück
Doppelsterne
Datenschutzerklärung
 

Berechnung der relativen Eigenbewegung von optischen Doppelsternen

J.S.Schlimmer (8/2008)

Optische Doppelsterne verraten sich nicht allein durch ihren großen Helligkeitsunterschied. In der Regel besitzen die Komponenten auch unterschiedliche Eigenbewegungen. Nachfolgend ist die Vorgehensweise zur Berechnung der Eigenbewegung skizziert. Die Berechnung der Eigenbewegung ermöglicht auch eine detaillierte Fehleranalyse aller Beobachtungsdaten des zu berechnenden Systems.

1. Datensatz aller Beobachtungsdaten für das Doppelsternsystem anfordern

Washington Double Star Catalog -> Data Request

Die benötigten Angaben "WDS DISC +  COMPS" sowie "WDS COORDS" entnimmt man direkt aus dem WDS Katalog. Für epsilon Lyrae findet man im WDS Katalog zum Beispiel folgenden Eintrag :
18443+3940STF2382AB    1777 2007  555  45 349   4.0   2.4  5.15  6.10 A4V F1V

WDS DISC + COMPS = STF2382AB
WDS COORDS = 18443+3940

2. Datensatz in Excel Tabelle importieren :

Den angeforderten Datensatz erhält man meist innerhalb von wenigen Tagen als Text Datei per email. Die Daten lassen sich leicht in Excel importieren:
Menü Daten -> Externe Daten importieren

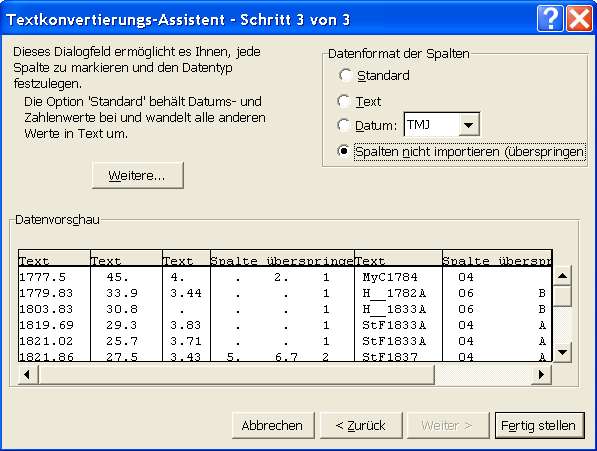
Abbildung 1 : Datenimport von epsilon Lyrae

Im ersten Schritt gibt man im Textkonvertierungs-Assistenten ein ab welcher Zeile die Daten importiert werden sollen. Im zweiten Schritt werden die Spaltenumbrüche definiert und im dritten Schritt (Abbildung 1) wird das Format - in dem die Daten importiert werden sollen - festgelegt. Hierzu werden die entsprechenden Spalten markiert und anschließend das Datenformat ausgewählt. Spalten, die nicht von Interesse sind, werden mit "Spalten nicht importieren" gekennzeichnet. Es empfiehlt sich alle Daten zunächst im Text Format zu importieren. In Excel können anschließend alle Punkte durch Komma ersetzt werden. Erst dann sollte man das Format für die Spalten wählen.

3. Korrektur für Positionswinkel durchführen

Damit die Darstellung der Beobachtungsdaten in Excel entsprechend der üblichen Konvention der Doppelsternbeobachtung entspricht, wird eine Winkelkorrektur durchgeführt :



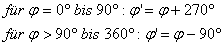
4. Umwandlung der Polarkoordinaten in Kartesische Koordinaten


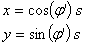
siehe Koordinatensysteme. Die Winkel müssen in Excel im Bogenmaß angegeben werden !

5. Diagramm

Die Eigenbewegung eines Sterns kann leicht dargestellt werden. Hierzu gibt es zwei verschiedene Möglichkeiten:

a) Zeitinvariante Darstellung

Die Eigenbewegung wird als xy -Plot dargestellt. Hierzu erfolgt zunächst eine Koordinatentransformation von Polarkoordinaten in Kartesische Koordinaten. Diese Art der Darstellung ist weit verbreitet und berücksichtigt Distanz und Winkel. Signifikante Messfehler fallen hierbei schnell auf. Die Zeit ist als Parameter nicht direkt ablesbar. Sie kann gegebenenfalls als Kommentar zu den Beobachtungsdaten hinzugefügt werden. Als Beispiel ist hier die Eigenbewegung von Delta Herkulis dargestellt. Herschels Beobachtung aus dem Jahre 1779 weicht dabei deutlich von der extrapolierten Ausgleichsgeraden ab.

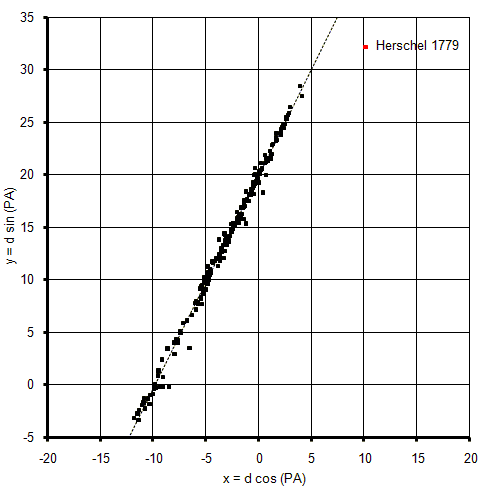
Abbildung 2: Eigenbewegung von Delta Herculis als xy-Plot


b) Zeitabhängige Darstellungen

Man kann die Eigenbewegung auch direkt über der Zeit auftragen. Allerdings benötigt man hierfür 2 getrennte Diagramme, da die Richtung im Betrag der Eigenbewegung nicht enthalten ist. Der Vorteil der zeitabhängigen Darstellung besteht darin, dass der Betrag der Eigenbewegung gleich der Steigung der Geraden ist. In dieser Darstellungsform werden signifikante Messfehler nicht so leicht erkannt, wie man aus den Beispielen von d Herkulis erkennt. Da die größte scheinbare Annäherung zwischen Delta Herkulis und dem Hintergrundstern um das Jahr 1964 erfolgte, ändert sich die Steigung der Geraden (theoretisch) sprungartig. Neben der Distanz muss zusätzlich auch der Winkel über der Zeit aufgetragen werden. Der Punkt mit der größten Steigung zeigt gleichzeitig den Zeitpunkt der scheinbar größten Annäherung an.

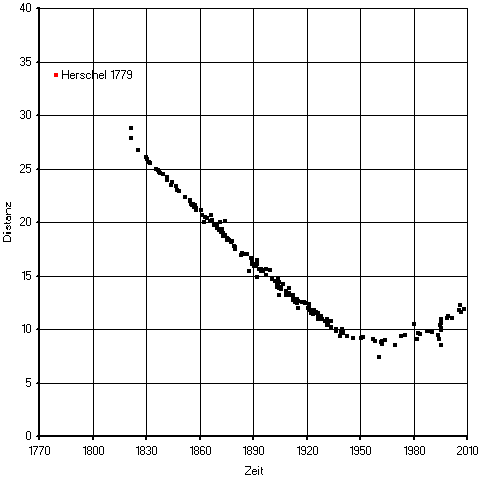
Abbildung 3: Scheinbare Distanz zwischen Delta Herculis AB über der Zeit


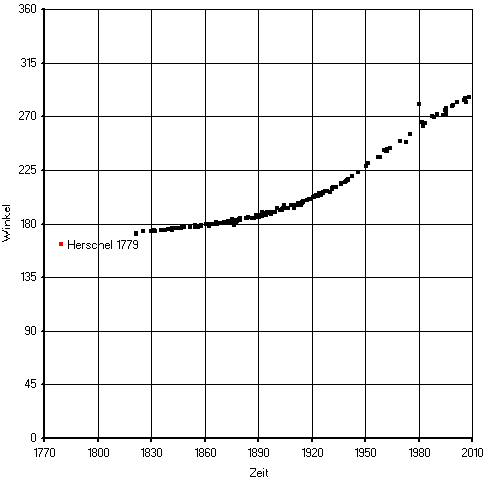
Abbildung 4: Winkel zwischen Delta Herculis AB über der Zeit


6. Ausgleichsrechnung

Die Possitionsmessung eines Doppelsterns beinhaltet drei Werte : Die Distanz (s), den Winkel (Phi) und den Zeitpunkt der Messung (t). Da alle weiteren Berechnungen in Kartesischen Koordinaten erfolgen, werden die Polarkoordinaten s(t), Phi(t) in x(t), y(t) umgewandelt. Beide Koordinaten x,y sind aber gleichermaßen fehlerbehaftet. Die Berechnung einer Ausgleichsgerade muss daher über eine multiple Regression erfolgen, die sehr aufwendig ist. Alternativ hierzu kann man auch je eine separate Ausgleichsgerade für x(t) und eine Ausgleichsgerade für y(t) berechnen. Aus diesen beiden Ausgleichsgeraden kann für jeden Zeitpunkt t ein korrigierter x,y Wert abgeleitet werden. Anhand dieser korrigierten x,y-Werte kann eine  dritte Ausgleichsgerade für den x,y Plot berechnet werden. Zur reinen Darstellung der Sternbewegung reicht aber meist die Berechnung von nur einer Ausgleichsgerade x über y aus. Dies ist der Fall wenn man die x,y Werte in ein Diagramm einträgt und eine Ausgleichsgerade durch diese Punkte berechnet. Dieser Fall ist hier nachfolgend skizziert.

Für die Beobachtungsdaten (x,y) wird eine Ausgleichsgerade nach der Methode der kleinsten Quadrate von Gauß berechnet. Die Meßfehler sollten dabei normalverteilt sein. Ausreiser entsprechen diesem Kriterium nicht. Sie haben einen erheblichen Einfluß auf die Ausgleichsrechnung und können das Ergebnis verfälschen. Sie sind jedoch leicht zu erkennen und werden vor der Ausgleichsrechnung eliminiert. Da es sich bei der Eigenbewegung um eine geradlinige Bewegung handelt, lassen sich die Beobachtungswerte leicht durch eine Gerade der Form


annähern. Die Koefffizienten a und b ergeben sich nach Gauß wie folgt [1] :




mit :

In Excel lassen sich diese Formeln leicht umsetzen. Man berechnet zuerst die Summen aller Xn, Yn Xn2, XnYn bevor man diese Werte in obige Gleichungen einsetzt.

7. Residuen

Mit der Geradengleichung können nun leicht die approximierten y' - Werte für jede Beobachtung berechnet werden. Hieraus werden die neuen Polarkoordinaten Distanz' und Winkel' abgeleitet. Mit Kenntnis dieser Werte können leicht die Residuen berechnet werden. Diese ergeben sich aus der Differenz der beobachteten und der berechneten Werte :


Die Residuen sind ein hervorragendes Maß für die Qualität jeder einzelnen Messung !
Beispiele
Quellennachweis

[1] Lothar Papula, Mathematik für Ingenieure 2, 5. Auflage 1990, Vieweg