www.epsilon-lyrae.de
zur Startseite zurück
Doppelsterne
Datenschutzerklärung

Inhalt:


Verschiedene Verfahren zur Kalibrierung des Abbildungsmaßstabes

Zur späteren Analyse von Doppelsternaufnahmen ist die genaue Kenntis des Abbildungsmaßstabes des optischen Systems notwendig. Hier werden verschiedene Verfahren gezeigt wie der Abbildungsmaßstab bestimmt und das optische System kalibriert werden kann.

1. Kalibrierung anhand bekannter Doppelsternabstände

Die einfachste Methode besteht darin, den Abstand mehrerer Doppelsterne aufzunehmen und mit den Angaben aus der Literatur zu vergleichen (siehe STFA 7 im Sternbild Stier). Hierbei stößt man jedoch schnell auf die Frage, welche Doppelsternsysteme für eine Kalibrierung in Frage kommen. Die Angaben aus den Katalogen sind in der Regel nicht aktuell und oft zu ungenau. Der Washington Double Star Catalog [1] bietet hierzu eine Liste von 80 Doppelsternen mit bekannter Umlaufbahn an. Anhand der bekannten Umlaufbahnen lassen sich auf den Tag genau die Ephemeriden berechnen, die zum Vergleich benötigt werden. Zu den aufgeführten Beispielen gehören Xi UMa, Epsilon Lyrae Cc-D, 70 Oph und STF3050 (Mayer 80). Gleichzeitig wird im Washington Double Star Catalog [1] aber auch vor dieser Methode gewarnt und auf die Methode mit einer Schlitzmaske -> siehe 3. Doppellochblende oder den Sterndurchgangstest verwiesen.


2. Transitmethode, Sterndurchgangstest

Bei der Transitmethode wird die Zeit bestimmt, die ein Stern zum Durchqueren des Bildfeldes benötigt. Die Umlaufzeit der Erde in Bezug auf die Fixsterne wird als Siderischer Tag bezeichnet. Er dauert  23 h 56 m 4 s = 23,93 Stunden. In 1 h legt also ein Stern am Himmelsäquator 360° / 23,93 h = 15,04° zurück. Da die Geschwindigkeit der Bewegung von der Deklination (der Abweichung vom Himmelsäquator) des Sterns abhängt, ergibt sich die Größe des Gesichtsfeldes allgemein zu :



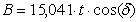
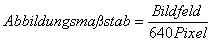
Ein Beispiel : Xi UMa benötigt bei etwa 3000 mm Brennweite im Durchschnitt 18,55 Sekunden um das Bildfeld der Webcam zu durchqueren. Mit einer Deklination von +31,5° ergibt sich ein Bildfeld von insgesamt 237,25''. Der Abbildungsmaßstab für die Webcam ergibt sich dann mit :

Zur Vermeidung von systematischen Fehlern sollten verschiedene Sterne unterschiedlicher Helligkeit und Deklination bei der Transitmethode verwendet werden. Die Ausrichtung der Webcam sollte parallel in Rektaszension sein. Bei größeren Abweichungen in der Ausrichtung bezüglich des Winkels sollte die Strecke entsprechend korrigiert werden. Winkel unter 5° wirken sich allerdings kaum auf das Ergebnis aus.

Vorteil der Transitmethode

Die Transitmethode bietet die Möglichkeit, unabhägig von anderen Werten und Berechnungen den individuellen Abbildungsmaßstab des optischen Systems zu ermitteln. Allerdings ist diese Methode mit einigem Aufwand verbunden, wenn der Abbildungsmaßstab mit großer Genauigkeit bestimmt werden soll. Die Genauigkeit des Abbildungsmaßstabes sollte dabei um etwa Faktor 10 besser sein, wie die geforderte Meßgenauigkeit.

Nachteil der Transitmethode

Um reproduzierbare Ergebnisse zu erhalten, sollte die mechanisch-optische Systemkonfiguration möglichst konstant und unempfindlich gegen äußere Einflüsse sein. Wird eine Barlowlinse verwendet, so wirkt sich der Abstand zwischen Linse und Bildebene - in der sich der CCD Chip oder die Skala eines Meßokulars befindet - direkt auf den Abbildungsmaßstab aus. Wird der Fokus anhand einer Skala festgehalten, lassen sich Änderungen leicht feststellen. Diese Anforderungen lassen sich in der Praxis mit einfachen Mitteln erfüllen.


3. Kalibrierung mit Hilfe einer Doppellochblende (Schlitztest)

Maskiert man die Teleskopöffnung mit einer Doppellochblende, so wird ein Stern durch jede der beiden Öffnungen (Aperturen) separat abgebildet. Im Brennpunkt überlagern sich die Lichtwellen beider Öffnungen und es entsteht ein typisches Interferenzmuster.


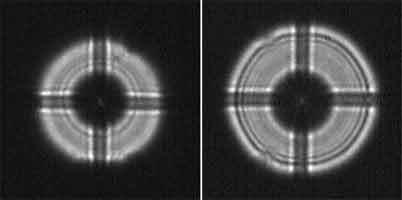
Abbildung 1 : Interferenzstreifen im Beugungsscheibchen, Abstand der Aperturen 8 cm

Der Streifenabstand f des Interferenzmusters hängt vom Abstand  B der beiden Öffnungen ab :


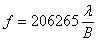
Der Quotient aus dem berechneten Streifenabstand f und dem aufgezeichneten Abstand in Pixel liefert sofort den gesuchten Abbildungsmaßstab. Das Problem des Verfahrens liegt darin, dass die Wellenlänge in der Regel nicht exakt bekannt ist. Zeichnet man Doppelsterne ohne Verwendung eines Filters auf, so sollte auch die interferometrische Kalibrierung ohne Filter erfolgen. Die effektive Wellenlänge hängt dann von der maximalen Empfindlichkeit des CCD Sensors und dem Spektrum des gewählten Teststerns ab.

4. Kalibrierung anhand der Eigenbewegung von Sternen

Gibt es für einen Stern mit großer Eigenbewegung genügend Messungen, so kann eine Ausgleichsgerade berechnet werden. Anhand der Geradengleichung kann für jeden beliebigen Zeitpunkt die Distanz zwischen den beiden Sternen berechnet werden. Damit läßt sich die zu erwartende Distanz auf jeden beliebigen zukünftigen Zeitpunkt extrapolieren. Mit einer eigenen Beobachtung kann anhand dieses Wertes das optische System kalibriert werden.  Im Frühling bieten sich hierfür Regulus im Löwen und Mayer 36 (SHJ 162) im Sternbild Jungfrau an.

Für Regulus lautet die Gleichung der Ausgleichsgeraden :


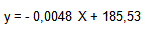
X  ist das Datum des Beobachtungszeitpunktes  z. B.  X = 2011,386

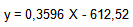
Für Mayer 36 = SHJ 162 lautet die Gleichung der Ausgleichsgeraden :


X  ist wiederum das Datum des Beobachtungszeitpunktes  z. B.  X = 2011,386

Mayer 36 bietet sich an, weil beide Komponenten etwa gleich hell sind. Nachfogendes Diagramm zeigt die Vorgehensweise :

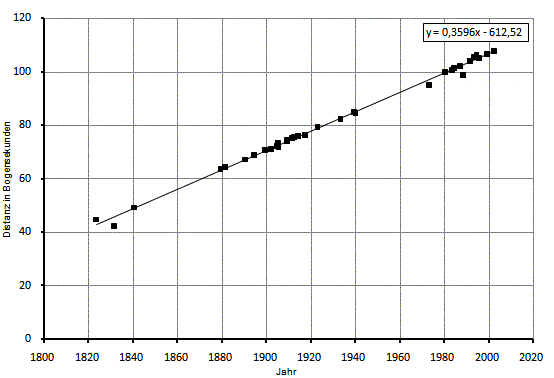
Abbildung 2: Distanz von Mayer 36 (SHJ 162) über der Zeit aufgetragen

Diese Methode ist der Transitmethode oder der Kalibrierung mit Hilfe einer Doppellochblende vorzuziehen.


5. Kalibrierung anhand optischer Doppelsterne mit zeitlich invariantem Abstand

Es gibt eine Reihe von Doppelsternen bei denen weder eine Änderung des Abstandes noch des Winkels über lange Zeit festgestellt werden kann. Diese zeitlich invarianten Doppelsterne sind ebenfalls für die Systemkalibrierung geeignet. Allerdings sollten sie gleiche scheinbare Helligkeiten besitzen, damit der Abstand hinreichend genau bestimmt werden kann.

Da alle Messungen fehlerbehaftet sind, ist es bei der Durchsicht eines Datansatzes auf den ersten Blick nicht offensichtlich, ob sich Abstand und Winkel im Laufe der Zeit ändern oder zeitlich invariant sind. Trägt man die Abstände über der Zeit auf und berechnet eine Ausgleichsgerade, so wird schnell deutlich ob sich die Abstände mit der Zeit ändern oder nicht. Geht die Steigung der Ausgleichsgeraden gegen 0, so reicht es in erster Näherung den Durchschnitt aller Messwerte als Wert für die Kalibrierung zu verweden.

Im Winter bietet sich hierzu Theta 2 Orionis an (nicht mit Theta 1 Orions = Trapezion zu verwechseln). Abbildung 3 zeigt die Abstandsmessungen von 1836 bis 2009. Der Betrag der Steigung der Ausgleichsgeraden beträgt nur 0,0007 Bogensekunden/Jahr. Die oben aufgestellte Forderung ist damit hinreichend erfüllt. Der Mittelwert der Abstandsmessungen beträgt 52,19 Bogensekunden. Die Steigung von Theta 2 Orionis AC hingegen liegt bereits bei 0,005 Bogensekunden/Jahr und ist damit fast 10 mal größer als die der Komponenten AB.


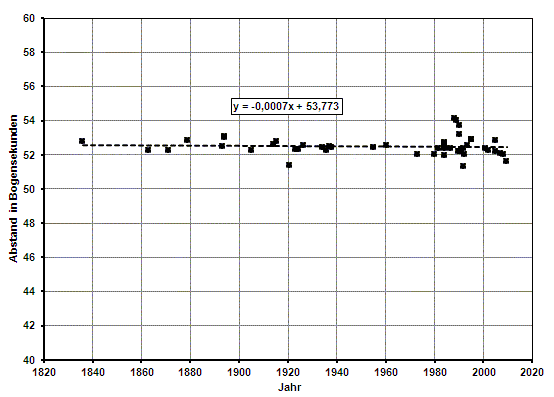
Abbildung 3 : Abstände von Theta 2 Oriones AB über der Zeit aufgetragen

6. Bestimmung des Korrekturwinkels

Der Korrekturwinkel muss immer neu ermittelt werden, wenn die Webcam neu montiert wurde. Zur Bestimmung des Positionswinkels sollte die Webcam an der Okularhülse möglichst exakt ausgerichtet werden. Bei einem Newton-Teleskop kann das mit Hilfe der Spinnenarme im intra- oder extrafokalen Beugungsbild eines Sterns erfolgen. Diese werden parallel zu den Bildrändern des Monitors ausgerichtet. Selbstverständlich sollten die Spinnenarme ihrerseits exakt in Deklination und Rektaszension ausgerichtet sein. Ohne großen Aufwand erreicht man mit dieser Methode Genauigkeiten von etwa 1° (Abbildung 3).

Abbildung 4 : mit Hilfe der intra- bzw. extrafokalen Beugungsscheibchen lässt sich bei einem Newton Teleskop die Webcam besonders einfach ausrichten. Die hier gezeigten Beugungsscheibchen wurden jeweils im gleichen Abstand vom Fokus aufgenommen. Die Abweichungen beider Beugungsscheibchen voneinander weisen auf Sphärische Aberration hin.

Eine weitere und sehr einfache Möglichkeit besteht darin, dass der Doppelstern bei ausgeschalteter Nachführung aufgezeichnet wird. Dabei wandert der Stern von Ost nach West (Transitmethode). Das Programm REDUC [3] kann aus den Einzelbildern des Videos automatisch den Korrekturwinkel berechnen und übernimmt diesen bei der späteren Auswertung der Aufnahmen. Die Genauigkeit liegt bei etwa 0,1°.



Abbildung 5 : Winkelkorrektur anhand der Einzelbilder eines Videos nach der Transitmethode mit dem Programm REDUC[3]. In diesem Beispiel wurden 150 Einzelbilder ausgewertet.
Weitere Links

Siehe hierzu auch : Fehleranalyse
Quellennachweis

[1] Brian D. Mason, Gary L. Wycoff, and William I. Hartkopf, The Washington Double Star Catalog, http://ad.usno.navy.mil/wds/
[2] REGISTAX, http://registax.astronomy.net/
[3] Florent Losse, REDUC, http://www.astrosurf.com/hfosaf/uk/tdownload.htm

Seitenaufrufe seit 1. Januar 2005 :